我们大家在小时候可能都玩过 “找路线”、“逃出迷宫”  这样的小游戏。通常的玩法一般是一开始顺着入口往后面走，遇到岔路口，就选择其中一条路往后走，走到此路无路可走的时候 ，就再退回到岔路口，然后再去选另外的一条路走，每次走到此条路不通时就返回到上一个岔路口另选一条路走 ......经历这般 “摸爬滚打”之后，最后才可能走到出口。容易想到以同样的思路递归实现迷宫问题。

首先，还是先来做准备工作，定义一个全局的二维数组表示迷宫、一个结构体变量表示坐标，如下

简单的迷宫（没有回路）

如下：

用递归的思路，容易想到 :从入口点开始，在与它相邻各个方向中找出一可通的位置，然后跳至该处并把此位置的值置为2，然后重复以上操作，划分子问题，当最后到达规定的出口时停止算法。

代码如下：

1 #pragma once 2 #include 
      
        3 #define N 7 4 int maze[N][N]={ 5     {
      0,0,0,0,0,0,0}, 6     {
      0,1,1,1,1,0,0}, 7     {
      0,1,0,0,0,0,0}, 8     {
      0,1,0,0,0,0,0}, 9     {
      0,1,1,1,1,0,0},10     {
      0,1,0,0,1,1,1},11     {
      0,1,0,0,0,0,0},12 };13 typedef struct Pos14 {15     int _col;16     int _row;17 }Pos;18 19 void PrintMaze(int arr[][N])20 {21     assert(arr);22 23     for(size_t i = 0; i< N; ++i)24     {25         for(size_t j = 0; j < N; ++j)26             printf("%2d ", maze[i][j]);27         printf("\n");28     }29     printf("\n");30 }31 int IsAccess(Pos cur, Pos next)32 {33     if(maze[next._row][next._col] == 134     && 0<= next._row && next._row < N35     && 0<= next._col && next._col < N)36     {37         return 1;38     }39     return 0;40 }41 void GetPath(Pos cur)42 {43     Pos next = cur;44     if(cur._col == N -1)  //找到出口45     {46         printf("出口:<%d, %d>\n", cur._row, cur._col);47         //return ;48     }49     maze[cur._row][cur._col] = 2;50    //向右走51     next = cur;52     next._col+= 1;53     if(IsAccess(cur, next))54         GetPath(next);55     //向上走56     next = cur;57     next._row-= 1;58     if(IsAccess(cur, next))59         GetPath(next);60   //向下61     next = cur;62     next._row+= 1;63     if(IsAccess(cur, next))64         GetPath(next);65     //向左66     next = cur;67     next._col-= 1;68     if(IsAccess(cur, next))69         GetPath(next);70     71 }
      

 

上面代码可以找出可通的路线，但是对于有多条路线的迷宫，此种方式不能找出一条最短的那条路线，并不理想。

继续往下优化 ~_~ ...

带环的多条线路迷宫，选择路径最短的一条线路

有一种比较巧妙的办法：改变记录迷宫线路的方式来实现。

思路：改变记录走过位置的标记方式。当前坐标位置的标记值是上一个位置的标记值加1

得到；（假如某个位置走过了，被标记为了4，那么走过的下一个位置就将其标记为5... ）

与此同时，这样的记录方式还有一好处就是间接的表示了一条路径的长度。 

由于改变了标记的方式，判断下个位置是否可通的条件做相应改变

判断可通条件：当前坐标的标记值 < 下一个坐标处的标记值 或者 下一个坐标标记值为 1

注意: 由于标记为 1的坐标也表示可通，所以初始时入口处坐标不妨从2开始标记。

实现代码：

1 #include "Stack.h"   //上次实现的栈头文件 2  3 int IsAccessInShortPath(Pos cur, Pos next) 4 { 5     if(( maze[cur._row][cur._col] < maze[next._row][next._col] || maze[next._row][next._col] == 1) 6     && 0<= next._row && next._row < N 7     && 0<= next._col && next._col < N ) 8     { 9         return 1;10     }11     return 0;12 }13 Stack shortPath;   14 void GetShortPath(Pos cur, Stack* pPath)15 {16     Pos next = cur;17     if(StackEmpty(pPath) == 0)                 //初始入口位置 记为218         maze[cur._row][cur._col] = 2;19     else20     {21         Pos prev = StackTop(pPath);     //当前位置标记值 为上一个位置标记值+122         maze[cur._row][cur._col] = maze[prev._row][prev._col] + 1;23     }24     StackPush(pPath, cur);25     if(cur._col == N -1)  //找到出口26     {27         printf("出口:<%d, %d>\n", cur._row, cur._col);28         //每找到一条路线就和shortPath里的路线比较长短29         //找到的路线更短，刷新shortPath30         if(StackSize(pPath) < StackSize(&shortPath)31             || StackEmpty(&shortPath) == 0)  //初始shortPath为空，需要刷新。32         {33             //不能直接shortPath._array = pPath->_array这样赋值34             //shortPath._array = pPath->_array;35             //shortPath._end = pPath->_top;36             //shortPath._top = pPath->_top;37             38             if(shortPath._array)//刷新shortPath，由于每次额外开辟空间来保存较短路径39                free(shortPath._array); //需要释放上一次开辟空间40             shortPath._array = (DataType*)malloc(sizeof(DataType)* pPath->_top);41             memcpy(shortPath._array, pPath->_array, sizeof(DataType) * pPath->_top);42             shortPath._end = pPath->_top;43             shortPath._top = pPath->_top;44         }45     }46     //向上走47     next = cur;48     next._row-= 1;49     if(IsAccessInShortPath(cur, next))50         GetShortPath(next, pPath);51     //向下52     next = cur;53     next._row+= 1;54     if(IsAccessInShortPath(cur, next))55         GetShortPath(next, pPath);56      //左57     next = cur;58     next._col-= 1;59     if(IsAccessInShortPath(cur, next))60         GetShortPath(next, pPath);61     //右62     next = cur;63     next._col+= 1;64     if(IsAccessInShortPath(cur, next))65         GetShortPath(next, pPath);66     //四个方向都走不通 开始回朔，pop掉path栈里保存的路径坐标67     StackPop(pPath);68 }

 

递归的过程可参考下图：

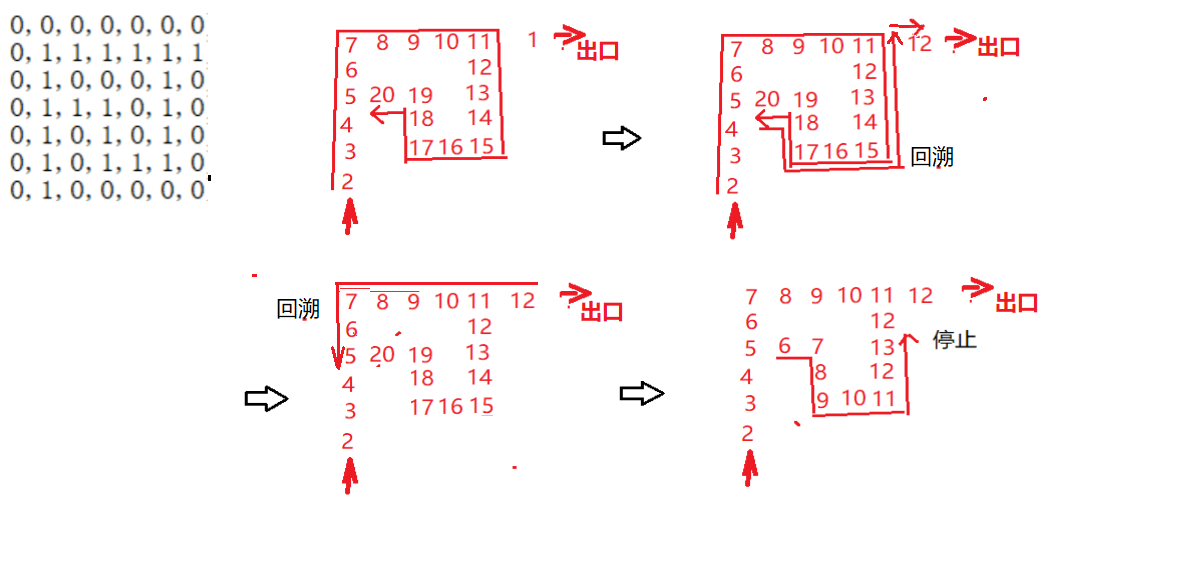
最后再简单测一下：

void TestMaze(){    Pos entry;    entry._col = 1;    entry._row = 6;    /*GetPath(entry);    PrintMaze(maze);*/    Stack path;    StackInit(&path);    StackInit(&shortPath);    GetShortPath(entry, &path);    PrintMaze(maze);    while(StackEmpty(&shortPath) != 0)    {        Pos cur = StackTop(&shortPath);        printf("(%d,%d)<-", cur._row, cur._col);        StackPop(&shortPath);    }    printf("入口\n");} 结果：

 

小结一下：

1.刷新shortPath里保存的路径，需要将path栈里存的路径整体拷贝过来。若将实现path栈底层的_array直接赋值给shortPath._array：

以本迷宫为例，它会先找到 ‘厂’ 型的路线，于是shortPath._array被赋值为path->_array，以此来保存路径；而在找第二条路径时 当递归到<4, 5>处递归结束，说明这条路径更长  shortPath._array存放的内容应保持不变(即上一条路径)，但在回溯查找该条路经时，shortPath有出栈操作，shortPath._array里内容会被改动； 而若是整体拷贝的话，每次都是新开辟空间来保持短路径，如若没到规定出口处，shortPath._array不会刷新，一直保存是一条最短的路径。

2.实现该迷宫时，默认设置出口为col = 6的位置，其实应该将出口的信息作为参数传入找路径的函数中，大家可以自行再优化。